物理の偏差値を65まで上げ、高校を卒業するまで維持した方法
私は高校時代、物理の記述式の模擬試験の偏差値を47から65まで約3ヶ月で上げ、卒業するまで65を維持することに成功した。その勉強方法を公開する。
また、大学卒業後、私と全く同じ勉強方法を物理の偏差値43の学生に教え、
見事に偏差値66となり、卒業まで偏差値66を維持し、達成した学生がいる。
私には偏差値43の学生を偏差値65まで上げる自信があった。
物理の偏差値43の学生を偏差値65に
上げる自信があったのはなぜか。
私は物理の偏差値43の学生に出会い、偏差値43から65に上げる自信が教える前からあった。
その理由は極めて簡単な原理から成り立っている。教える前、学生にこう話したのだった。
『私は自分自身、頭は良くない。人はすべて同じ物質で構成され、同じ物質からできている。
脳の化学反応の仕方の基本原理も同じだ。だから、自分と全く同じ勉強方法を学生に行えば、
必ず学生は自分と同じ偏差値65までは上がるはずだ。』
と断言した。
事実、私の教えを忠実に守ったその学生は偏差値66まで上がり、偏差値65を維持したのだった。
私の考え方は的中した。成績の上がり方までそっくりだったのを覚えている。
物理の偏差値65を維持した実績のある勉強方法の黄金律
・6割から7割解ける問題集を選べ。
これは非常に重要で、6割から7割解ける問題集がなければ勉強する意味が
ないといっても過言ではないだろう。私は偏差値47の時、
徹底的に理解できる参考書と問題集を探した。理解ができなければ、
応用が全くできないため、勉強した問題しか解くことができない。
また、理解できなければ、物理や数学の記憶に一番適した
エピソード記憶を形成することもできないだろう。
そのようにならないためにも、徹底的に理解できる参考書と問題集を探す必要がある。
理解できるか理解できないかを見極めるコツは、
自分が過去に勉強して理解できている問題の解説を見ればよいだろう。
その解説方法が自分にとってしっくりとこなければ、他の問題集を探した方がよい。
参考書を選ぶ場合も同様に探す作業が必要だ。
・分野ごとに徹底的に学べ。
これも非常に重要である。様々な分野を同時並行して勉強すると、
その分野の表面的な問題、すなわち、簡単な問題はすらすら解けるように
なるかもしれないが、奥深い難しい問題までは手を出すことが難しくなることだろう。
様々な問題を同時並行して問題を解いていく場合、難しい問題を解く頃には
簡単な問題の解法を忘れてしまっているため、難しい問題がさらに
難しく感じることだろう。
私の経験からこれは言えることだが、簡単な問題の解法が大量に頭の中にはいると
自然と難しい問題の解法が見えるようになるのである。
それは、難しい問題が簡単な問題の組み合わせでできていることを意味する。
私は1冊の問題を繰り返し学ぶことはおすすめしない。
4冊程度集め、4冊から同じ分野を集め、徹底的に1つずつ分野を勉強する。
すらすら解けるようになったら、次の勉強を行うようにする。
偏差値65を維持するときに使用した問題集は教科書以外に4冊である。
この4冊で徹底的に分野ごとに勉強した。例えば、運動法方程式ばかり1ヶ月解くなどである。
・自分の中で解くための理論を持ち、すべての問題が解ける理論を完成させよ。
ほとんど内容の変わらない易しい問題を徹底的に集め、
すべて理解できるまで次の問題をやらない。
理解できない問題は、必ず誰かに聞き、完全に理解すること。
また。聞ける状態になるまで、自分の中で仮説を立てて無理矢理
理解させて勉強を進める。
同じような問題を解き、同じ仮説でその問題がその問題が説き明かせるか
チェックする。もし解けなかった場合、仮説のどこが誤っていたのか誤っていたのか
考え、どのように仮説を立て直せば今までの問題を矛盾なく解くことができるか
考える。このようにして必ず自分の仮説で閉じた世界を広げるように勉強すると、
自然と間違った理由、解けなかった理由が自分の理論から導き出せるようになる。
難しい問題がだんだん解けるようになる原理であるため、極めて重要な考え方だ。
似たような問題に出会ったとき、どこまでが似ていて、どこから新しいのか自分の中の世界と
照らし合わせるように勉強を進めていくのだ。
・絶対に負けたくないというライバルを持て。
私は初めて物理の試験を受けたとき、クラスの平均点以下だった。
私はライバルよりは明らかに勉強しているつもりだったが
ほとんど勉強してないライバルが高得点をとっていたのだ。
その時、くそ~負けてたまるか~!と心の底からとてつもなく強く思ったものだ。
その思いが強ければ強いほど勉強意欲がわくため、非常に効果的である。
試験結果をもらった次の日から平日は毎日物理に2時間、土日は物理に
20時間つぎ込みむようになり、3ヶ月後、見事、偏差値65となった。
ライバルはここまで勉強していないことをいつも会話の中から探っていた。
・短期間に数多くの類似した問題を解け。
短期間に数多くの類似した問題を解く。これは頭の中を柔軟にさせ、
応用問題が解けるレベルに成長させるのに不可欠な要素である。
実は類似した問題を沢山とかなければダメだ。
脳の構造として、人は関連して物事を覚えているため、類似した問題を数多く解くことは
脳科学的に大変効果的である。また、短期間に同じような情報を脳に送ることによって
脳に必要な問題であると判断させ、長期記憶を形成させることができる。
実はこの長期記憶こそ偏差値65を維持するための重要なポイントとなるのである。
・忘却曲線を意識し、長期記憶を増やせ。
勉強は復習しなければ忘却曲線により忘れていってしまう。
偏差値65まで上がる人と上がらない人の決定的な差は効果的な復習時期を選んでいるか
がポイントとなる。長期記憶を形成させてれば、なかなか忘れていかないため、
勉強すればするほど加速的に成績が伸びる時期がやってくる。
ただし、長期記憶は条件が整わないと形成されない。
その長期記憶形成の条件となるのが復習時期である。
復習の適切な時期はいつか。
復習するのにもっとも適切な時期はいつか検討する。5週間目にテストがあるとする。
記憶量を最大にしておきたいものだ。
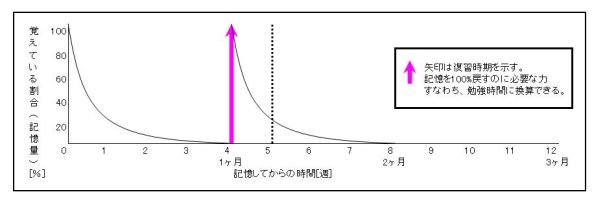
・1ヶ月後に復習をする場合
人は初めて覚えたことは1ヶ月で完全に忘れる。よって、1ヶ月後に復習をしても
長期記憶は形成されない。記憶量はこの波形を繰り返すことになるだろう。
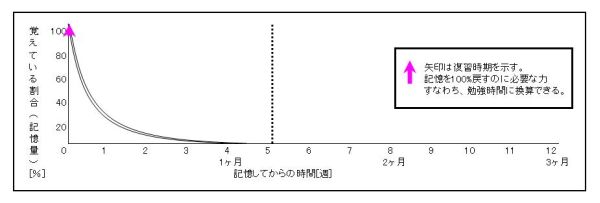
・1分後に復習する場合
1分後に復習をしたらどうなるか。忘却曲線の記憶量の減少率はほどんど変化しない性質がある。
完全に覚えているうちに復習をしても効果はない。5週間後には覚えていない。
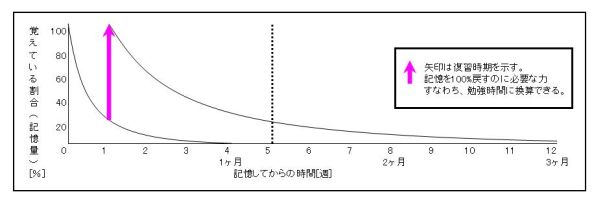
・1週間後に復習をする場合
脳科学的に第1回目の復習がもっとも適しているのは1週間後であると言われている。
忘却曲線がのびているのがわかるだろう。記憶量が完全になくなるまでに時間を要すようになる。
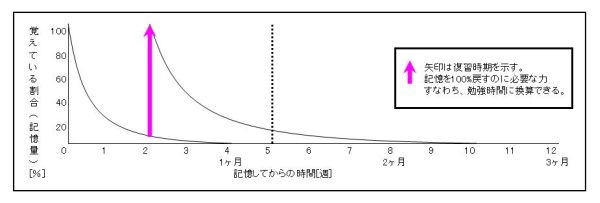
・2週間後に復習をする場合
忘れ掛かった時期をねらうと忘却曲線はのばすことができるとは言われているが、
1ヶ月、すなわち、4週間経つとすべての記憶量が失われることを忘れてはいけない。
従って、1週間後に復習したときよりも、忘却曲線の伸び率は下がっていくのである。
・3週間後に復習をする場合
3週間後はもうほとんど記憶に残っていない状態である。
実は今まで説明をしてこなかったが、ピンクの矢印の大きさは記憶を100%に戻すのに必要な力、
すなわち、勉強時間に換算することができるものなのである。
1週間後に復習していれば勉強の労力はそれほど掛からないが、3週間後はほぼゼロに
等しいため、多くの勉強の労力を必要とするのである。
しかも、忘却曲線の伸び率は最低だ。1ヶ月後、すなわち、4週間後の忘却曲線と同じ波形に
近くなるのである。
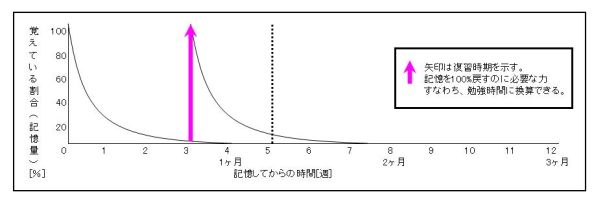
・4週間後に復習をする場合
4週間経つとすべての記憶が失われているので、もう、説明するまでもなく、
長期記憶を形成されられない無意味な復習時期である。
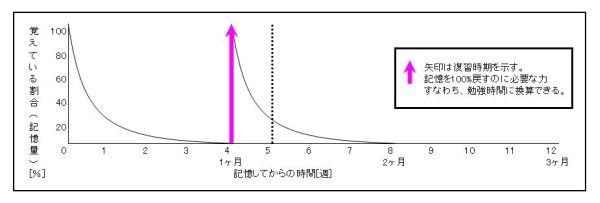
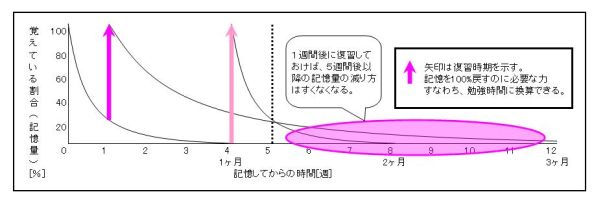
5週間後に記憶量が一番多いのはどれか。
今まで説明してきた図を合成したものである。
ここで注目して欲しいのが1週間後に復習した場合と、4週間後に復習した場合、
5週間目時点では、記憶量に差がほとんど見られないことである。
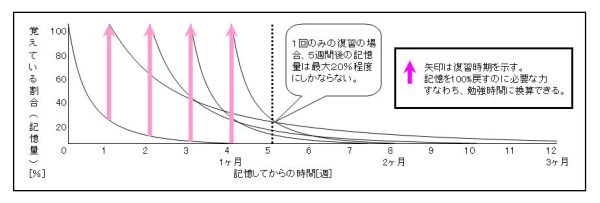
1週間後と4週間後の復習のみ取り上げてみた。
その後の忘却曲線の減り方に注目して欲しい。
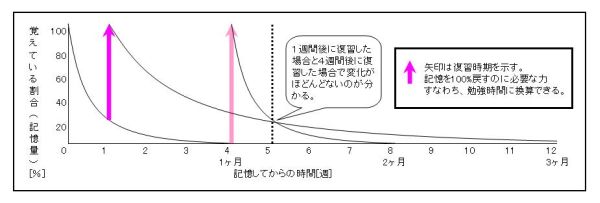
脳科学的にもっとも効率が良いと言われている1週間後に復習した方が
忘却曲線の伸び率は断然違うのである。
このように、偏差値65を維持して行くには忘却曲線を徹底的に意識して勉強しなければ
ならないのである。
ただ、ここで気になるのが5週間目の記憶量が低すぎるという点だ。
これを向上させるにはどうしたらよいのか。
すでに研究者のなかで研究が行われ、復習は適切な時期に3回行えば
ほぼ長期記憶を形成できると言われている。
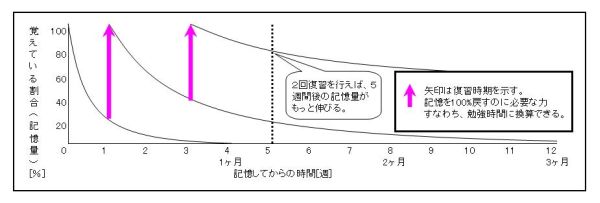
・2回復習をした場合、忘却曲線はどうなるか。
1週間後に1回目の復習、その復習から2週間後に2回目の復習を行った場合の
忘却曲線の減り方は緩やかになる。
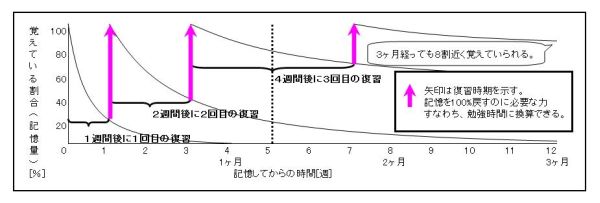
脳科学的にもっとも効率の良い復習時期
1週間後に1回目の復習、その復習から、2週間後に2回目の復習、その復習から4週間後に
3回目の復習を行うことが脳科学的にもっとも効率の良い復習時期であることが研究で
確認されている。この時期をねらった勉強計画を立てれば偏差値65も夢ではない。
最後に重要なこと。
私は短期間に類似した数多くの問題をこなすという週間により、自然と復習をしていたようである。
それが偏差値65を維持することができた大きな要因だと考えている。
また、偏差値65レベルまで勉強が進んだことにより、勉強することが楽しくなった。
これが最終的に偏差値65を維持することができた理由と考えられる。
この原理は私だけでなく、この原理を教えた学生が私と物理の偏差値をたたき出したと言うことだ。
これはまぎれもない事実なのである。
その学生も私と同じシナリオをたどった。物理の勉強は楽しいと。。。
では、すべての黄金律を守るためにはどうしたらよいか。
⇒『TimeSelector』という受験勉強専用のスケジューラがある。
限られた時間の中で勉強をしなければならない。
どんなに隙間時間を差がしても時間は有限である。
その有限の時間を徹底かつ有効的に使用できるようにするために勉強計画ソフト
『TimeSelector』を開発した。私が高校時代から研究をしていたソフトである。
このソフトは脳科学的にもっとも効率の良い復習効果を生む時期をコントロールできる機能
を持っている。あなたも、このソフトで成功を勝ち取って欲しい。
学生は物理の勉強の他、英語の勉強、数学の勉強も同時にやっていかなければならない。
要するに、バランスよく勉強を進める力が要求されるのである。
『TimeSelector』では復習の勉強をバランスよく進めていくスケジュールが組めるのだ。
試験日までに大量の問題をすべて解ききることができるか不安になるものである。
『TimeSelector』を使えば、長期スケジュールを見通すことができる。
しかも分単位の緻密なスケジュールで組めるのだ。
電車の中でできる勉強も無駄にしたくない。小さなメモ帳を買えば、電車の中でも勉強できる。
でも、数学の難しい問題よりは数学の簡単な問題を電車の中で行いたい。
そんな計画をしたくなる。
『TimeSelector』を使えば、電車の中でできる勉強と自宅でできる勉強を考慮して
勉強計画を組めるのだ。
本番と同じような模擬の試験勉強時間を作りたいものだ。
『TimeSelector』を使えば、一括指定機能により、まとまった時間を確保することができるのである。
予定が狂ったときに勉強計画を立て直したくないものだ。
『TimeSelector』を使えば、ボタン1つでスケジュールの組み直しができる。
電車の中で何気なく勉強するのではなく、それを計画の一部にしたい。
『TimeSelector』は電車の中の時間を長期スケジュールの一部にできるのだ。
勉強がどれだけ達成したのか毎日把握したい。
『TimeSelector』を使えば、どれだけ勉強が完了したのか毎日分かるようになっている。
具体性のある分単位の緻密なスケジュールは失敗する可能性が低い。
毎日持ち歩きたいものだ。
『TimeSelector』を使えば、携帯にスケジュールを送信できるので、毎日持ち運べるのだ。
『TimeSelector』について
『TimeSelector』のホームページへ移動 ←クリック
※『TimeSelector』のフリーエディションは無料でダウンロードできます。